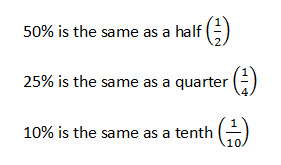Percentages
Percent comes from the Latin word "percentum" which can be translated as "by the hundred". 100 percent is the value given to a whole amount and this is the key to dealing with percentages. The symbol for percent is % and I will be using this throughout the lesson. Percentages are used frequently in everyday life and a good understanding of them can be very beneficial.
Percentages, decimals and fractions
These three are all just different ways of expressing numbers. If you can convert quickly between percentages and one of the other values then your percentage calculations can be significantly sped up. Here are some common percentage conversions that you should take the time to learn.
Converting a percentage into a decimal is very straightforward if you remember that percent means 'out of 100'. Take the percentage you're trying to find and divide it by 100 to find the equivalent decimal
|
50% is 0.50 (we usually write 0.5 for speed)
25% is 0.25 10% is 0.1 5% is 0.05 1% is 0.01 32% is 0.32 113% is 1.13 246% is 2.46 |
Obviously this is just a small number of percentages to give you an idea of the process but I hope you've got the idea by now.
Non-Calculator strategies
Most of the time we have a calculator handy (on our phones, for example) but it is still worthwhile knowing how to calculate percentages quickly without one. You can use the conversions above as a starting point and build up from there

50%
Since this is the same as a half the quickest way to find 50% of a number is to halve it (divide by 2).
Eg. 50% of 24 is 12.
Since this is the same as a half the quickest way to find 50% of a number is to halve it (divide by 2).
Eg. 50% of 24 is 12.

25%
Using the information above this is the same as a quarter so the quickest way to get there is to divide by 4, however most of my students prefer to think of it as half of 50% instead. This means you can take your original number and halve it then halve it again to calculate 25%.
Eg. 25% of 24 is 6
Using the information above this is the same as a quarter so the quickest way to get there is to divide by 4, however most of my students prefer to think of it as half of 50% instead. This means you can take your original number and halve it then halve it again to calculate 25%.
Eg. 25% of 24 is 6

75%
As shown in the picture to the left, 75% is the same as three quarters. Another way to think about this is 50% + 25% so if you can calculate those other two percentages you can easily add them together to reach 75%. Of course you're more than welcome to just calculate three quarters directly!
Eg. 75% of 24 is 18.
As shown in the picture to the left, 75% is the same as three quarters. Another way to think about this is 50% + 25% so if you can calculate those other two percentages you can easily add them together to reach 75%. Of course you're more than welcome to just calculate three quarters directly!
Eg. 75% of 24 is 18.

10%
10% is the same as one tenth of the whole amount so to calculate 10% of a number you need to divide by 10.
Eg. 10% of 24 is 2.4
10% is the same as one tenth of the whole amount so to calculate 10% of a number you need to divide by 10.
Eg. 10% of 24 is 2.4

1%
You might have already guessed but you can calculate 1% by dividing the whole number by 100. Other strategies include dividing your 10% by 10 again but that's just an extra calculation which means there's more of a chance you'll get it wrong!
Eg. 1% of 24 is 0.24
You might have already guessed but you can calculate 1% by dividing the whole number by 100. Other strategies include dividing your 10% by 10 again but that's just an extra calculation which means there's more of a chance you'll get it wrong!
Eg. 1% of 24 is 0.24
Once you have these calculations sorted you can build up to any other percentage in just a few steps.
- 20% is double 10% so take your 10% answer and multiply it by 2.
- 5% is half of 10% so divide your 10% value by 2.
- 2% is double 1% (I'm sure you get the drift by now...)
- 0.5% is half of 1%
- 60% is 50% + 10%
- 90% is 100% - 10%
- 200% is double 100%
- 35% is 10% + 10% + 10% + 5% (or if you prefer you can do 3 x 10% + 5%)
Using a Calculator
Now you have a good understanding of what percentages are it's time to speed up your calculations a little. some calculators have a percentage button but they each work in a different way and to be honest I've never bothered to learn how they work. Instead it is just as quick to use something called a 'multiplier'. As the name suggests, the multiplier is a number you multiply the 100% value by to find an answer. The multiplier is the decimal equivalent of the percentage you need to find as discussed earlier in the lesson.
|
Example 1:
Find 35% of 24 Multiplier: 0.35 Calculation: 0.35 x 24 = 8.4 |
Example 2:
Find 64% of 112 Multiplier: 0.64 Calculation: 0.64 x 112 = 71.68 |
Example 3:
Find 235% of 19 Multiplier: 2.35 Calculation: 2.35 x 19 = 44.65 |
Percentage increase and decrease
The most usual time to see a percentage is during a sale or when calculating interest rates. In a sale the percentage is to be taken off the original amount (percentage decrease) and interest is when money is added into your account (or the amount extra you need to pay on a loan) so the percentage needs to be added on (percentage increase). There are two ways to solve problems like these and you should pick the method you find easier to understand:
- Calculate the percentage then add it on or take it off the original as appropriate.
- Calculate the multiplier which takes the percentage change into account already.
Example 4:
House prices have gone up by 4% in the past year. My house was valued last year at £125,000. What is it worth now?
House prices have gone up by 4% in the past year. My house was valued last year at £125,000. What is it worth now?
|
Method 1
Multiplier: 0.04 Percentage: 0.04 x 125000 = 5000 Add it on: 125000 + 5000 = £130,000 |
Method 2
100% + 4% = 104% Multiplier: 1.04 Calculation: 1.04 x 125000 = £130,000 |
Example 5:
In a sale a TV is reduced by 20%. Before the sale the TV was priced at $450. How much will it cost me in the sale?
In a sale a TV is reduced by 20%. Before the sale the TV was priced at $450. How much will it cost me in the sale?
|
Method 1
Multiplier: 0.2 Percentage: 0.2 x 450 = 90 Take it off: 450 - 90 = $360 |
Method 2
100% - 20 % = 80% Multiplier: 0.8 Calculation: 0.8 x 450 = $360 |
So now you know all there is to know about percentages (well, enough of it to get by!) it's time to tackle the homework. Have fun!