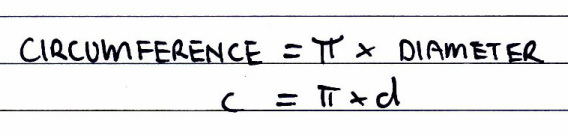Circles
Although much of this lesson could have been in the Area and Perimeter section I thought it deserved a lesson of it's own as the humble circle is pretty awesome. There are few shapes that have so many key words associated with them so we'll start with some definitions.
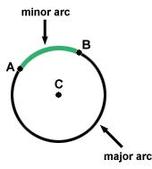
Parts of the Circle
|
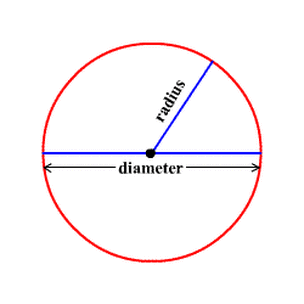
The line joining the centre of the circle to the outside edge is called the radius. This line is important when calculating the area of a circle (see below).
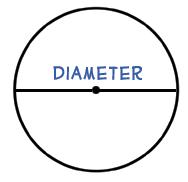
The line from one side of the circle to the other, going through the centre is called the diameter. Notice that the diameter is twice the length of the radius. |

The distance all the way around the outside of a circle is called the circumference. This is the same as the perimeter of a circle but is assigned a separate name for some reason! The formula for calculating the circumference of a circle is explained below
|
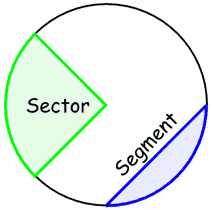
Two regions of a circle which often get confused are sector and segment.
A sector is created by an arc and two radii and looks a little like a cheese wedge or a slice of pie. A segment is created by a chord and arc and looks like a piece of orange (also called a segment!) Try not to confuse them please! |

The last line of interest, pictured here, is a tangent. A tangent hits the outside of a circle and bounces off. It does not cross inside the circle and only touches the circumference once.
A note about Pi...
Before we go any further it's important that you have an understanding of the number that is pi (pronounced pie). With a greek name and a greek symbol to represent it, pi is an irrational number (this means it goes on forever without finishing). Pi caused the greeks an awful lot of problems when they were trying to find the area of a circle and they had to radically change their belief that all numbers could be written as fractions or decimals that stopped. The closest fraction they could find was 22/7 but this just wasn't quite accurate enough. At the time of writing this lesson pi has been calculated to 12.1 trillion digits; a feat which took 94 days! You don't need to know any of these (although people do like to try and memorise pi to as many digits as possible) as pi is stored on all scientific calculators to a good degree of accuracy. Usually you need to press the shift or second function button first - make sure you know where pi is on your calculator!
Circumference
As mentioned at the start of this lesson, the circumference is the mathematical name for the perimeter of a circle. To find the circumference you need the following formula:
Remember you can use the value of pi stored on your calculator. If you don't have a scientific calculator (which you all should have since you have either windows calculator or mac calculator as shown above) then the common convention is to use the value 3.14 for pi.
|
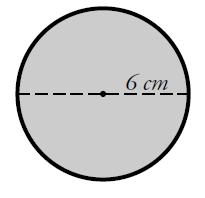
Example 1: Find the circumference of this circle
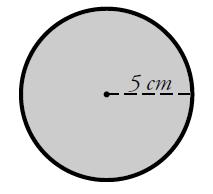
Circumference = pi x 6 = 18.8 cm (1dp) NOTE: The exact answer given on the calculator was 18.849555921538759... but writing out all of that (or more) would have been a bit ridiculous. Instead I have rounded my answer to one decimal place (which is why I wrote 1dp after my answer). If you're not sure how to do this look here. Example 2: Find the circumference of this circle
Remember that the circumference formula needs the diameter. This circle has got the radius included so you need to first calculate the diameter. Double the radius to get a diameter of 10. Circumference = pi x 10 = 31.4 cm (1dp) |
|
Area
By now you should know that the area is the space inside a shape. The area of a circle is found using another formula involving pi and the radius:
Remember from the Types of Numbers lesson that this end part means "r squared" which is the same as saying "r x r". So the formula could be rewritten as Area = pi x radius x radius.
Now it's time for you to do some maths! Click the link below for the homework and extra credit.