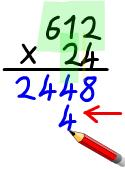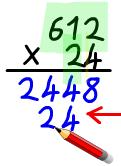Multiplication
Times tables
There's a lot to be said for learning your times tables. Believe it or not I was never made to learn my tables so didn't until I started teaching and suddenly had to know them! I wish I'd put the time in and learnt them earlier in my life but as there was nothing I could do about this then I got to work learning them at the age of 22.
Some are easier than others. The twos, fives and tens shouldn't take too much work, then the threes and fours need to be learnt followed by the rest. The key is to look for tricks. I'm not saying there's a cheat for all the times tables but here are a few I know
Some are easier than others. The twos, fives and tens shouldn't take too much work, then the threes and fours need to be learnt followed by the rest. The key is to look for tricks. I'm not saying there's a cheat for all the times tables but here are a few I know
|
Twos - Doubling
Remember that the two times table is made up entirely of even numbers. |
Consecutive numbers
12 = 3 x 4 56 = 7 x 8 |
Tens - All end in zero.
4 x 10 = 40 9987 x 10 = 99870 etc. |
|
Symmetrical
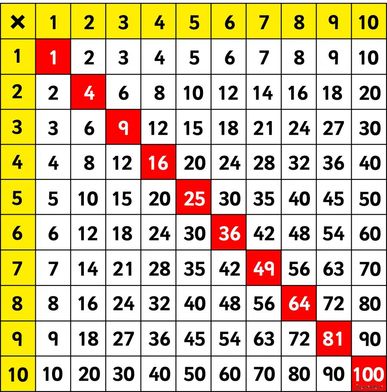
6 x 8 is the same as 8 x 6 so you only need to learn half your tables! Use a times table grid to help you (see below) |
Fives
Always end in 5 or 0 Half the 10 times table |
Elevens
Just repeat the number you're multiplying from 1 x 11 = 11 until 9 x 11 = 99. After that you need to look for another trick! |
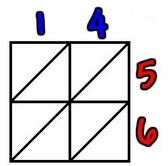
Times table grid - up to 10 x 10
Multiplication Methods
When I was at school there was only one way to multiply - the column method. Nowadays students are taught lots of different methods which get to the same answer so I want to share a few new techniques with your here.
Traditional Column Method
This is probably the method you're most familiar with. It requires you to totally multiply one number by part of the second, then moving on, adjusting for the fact that you're now in the tens column.
An example will make things clearer!
This is probably the method you're most familiar with. It requires you to totally multiply one number by part of the second, then moving on, adjusting for the fact that you're now in the tens column.
An example will make things clearer!
|
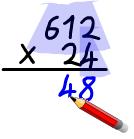
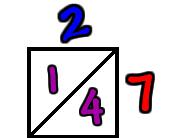
Example: 612 x 24
Step 1: Muliply 612 by 4. Always start from the right when multiplying and work backwards so you can carry any tens into the next column as needed. Step 2: Multiply 612 by 20. To do this you only need to multiply each part by 2 but be carful where you write your answer. Some people like to fill up the gap under the 8 with a zero since you're multiplying by 2 and 10. |
You'll note that this example didn't need you to carry over any tens since you had single digit answers until it didn't matter. If you were multiplying 617 x 24 you would have got 14 for your first multiplication. Write the 4 in the same spot you put the 8 last time and 'carry' the one. This simply means it will get added to whatever your next answer is, so when you do 1 x 4 = 4 you must write an answer of 5 (as 4 + the carried 1 is 5). With practise this becomes natural so don't worry!
Box Method
This quick and easy method is the one most often taught in primary school at the moment. It doesn't rely on any understanding and all you need to know is how to multiply single digit numbers and adjust for the zeros. What you're really doing is working with "place value" and like the method before filling the gaps with however many zeros you need to make the sum correct. I'll show you another example.
This quick and easy method is the one most often taught in primary school at the moment. It doesn't rely on any understanding and all you need to know is how to multiply single digit numbers and adjust for the zeros. What you're really doing is working with "place value" and like the method before filling the gaps with however many zeros you need to make the sum correct. I'll show you another example.
|
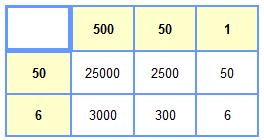
Example: 551 x 56
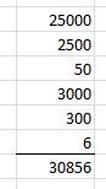
Step 1: Split your numbers up into the component parts and write these around the edge of your box. The size of the box will depend on the multiplication you are performing but a 3 digit by 2 digit question requires a 3 by 2 box. Step 2: Multiply your numbers together. For 50 x 500 you need to do 5 x 5 = 25 first, then add in the three extra zeros to get the correct answer of 25000. This goes in the first box where the 50 and the 500 meet. Step 3: Repeat step 2 until your box is full. This method has the benefit of making sure you don't miss out any multiplications as if you have any blanks you know you're not yet finished! Step 4: Add up the contents of your box to get your answer. I recommend writing out your numbers, lining them up on the right (just like excel does!) and using column addition to get your final answer. This is especially important if your numbers are large or you have lots of them. 551 x 56 = 30856
|
Lattice Multiplication (aka Chinese Method)
The final method is my favourite and since I've learnt it I can multiply huge numbers together very quickly. It takes a little while to get used to and the set up can sometimes take longer than the actual maths but there are no zeros to deal with meaning as long as you know your times tables up to 9x9 you can use this method to do any muliplications.
|
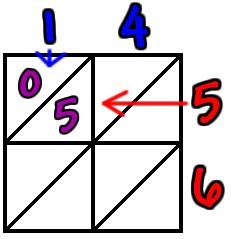
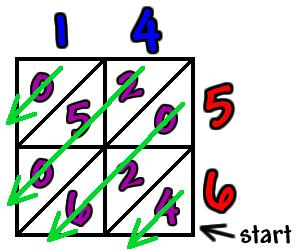
Example: 14 x 56
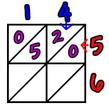
Step 1: Draw a grid with enough boxes for your multiplication and write the single digit components around the outside. Draw diagonal lines through each of your boxes as shown above so you can separate the tens and the ones. Step 2: Now you have set up your grid the multiplication can begin. Take each multiplication in turn, writing your answers either side of the diagonal line until the grid is complete. Remember single digit answers will have zero in the tens column and you can complete the multiplications in any order as long as you complete the grid. Step 3: Add up the diagonal stripes, starting at the bottom right and working your way back up to the top. Put your answers underneath and to the left then read off your answer top to bottom, ignoring the zero at the beginning. 14 x 56 = 784
|
When your adding up the diagonals you will often get a number greater than 9. Just like before you must carry the one so in this case that means you add it into the next diagonal. Remember you can only have one number in each box, even when doing the answers. So 247 x 38 is 9386, not 81386. Try this one for yourself so you see what I mean. (Start this one with a 3 by 2 grid)
Well done for making it through this lesson. You deserve a rest now but unforunately there's still the homework assignment to do! Good luck!