Types of Number - Due 14th June, 23:59 HOL time.
Please send all your work to [email protected].
Send Homework and Extra Credit together or separately, whichever is easier for you.
Please put "Number Types - HOL ID" in the subject line.
Remember to include your HOL username, ID and House in the main body of your email.
Do not send attachments as they will not be opened.
Send Homework and Extra Credit together or separately, whichever is easier for you.
Please put "Number Types - HOL ID" in the subject line.
Remember to include your HOL username, ID and House in the main body of your email.
Do not send attachments as they will not be opened.
Homework
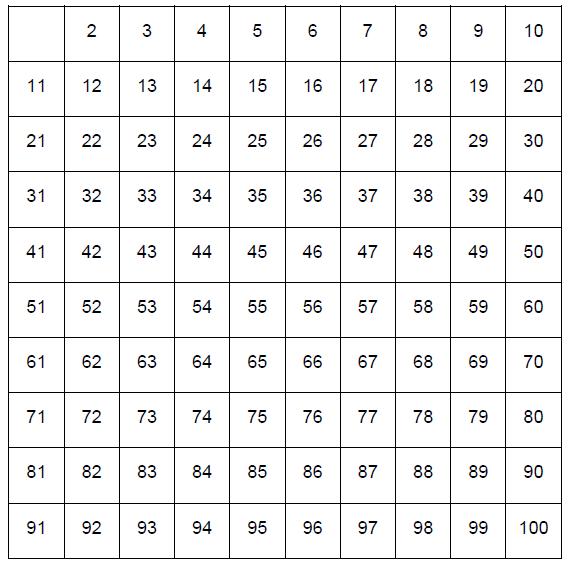
The Sieve of Eratosthenes - 15 points
This method of finding prime numbers was discovered by the Greek mathematician Eratosthenes in around 240 BC. It is a very elegant way of removing all the non prime numbers by looking at multiples. Follow the instructions below by shading in the grid provided then send me a copy of your completed grid and a list of all the prime numbers below 100.
This method of finding prime numbers was discovered by the Greek mathematician Eratosthenes in around 240 BC. It is a very elegant way of removing all the non prime numbers by looking at multiples. Follow the instructions below by shading in the grid provided then send me a copy of your completed grid and a list of all the prime numbers below 100.
Step 1: Circle the number 2 (this is prime) then cross out all the multiples of two (they are not prime)
Step 2: Circle the next number which isn't already crossed out (3) then cross out all its multiples.
Step 3: Circle the next number which isn't already crossed out (5) then cross out all its multiples.
Step 4: Circle the next number which isn't already crossed out (7) then cross out all its multiples.
Step 5: You're done! All the numbers which haven't been crossed out yet are prime numbers. You can circle them if you wish!
NOTE: If you had a bigger grid you might need to keep going a little longer but for a 2-100 grid this is all that is needed.
Step 2: Circle the next number which isn't already crossed out (3) then cross out all its multiples.
Step 3: Circle the next number which isn't already crossed out (5) then cross out all its multiples.
Step 4: Circle the next number which isn't already crossed out (7) then cross out all its multiples.
Step 5: You're done! All the numbers which haven't been crossed out yet are prime numbers. You can circle them if you wish!
NOTE: If you had a bigger grid you might need to keep going a little longer but for a 2-100 grid this is all that is needed.
Factors and Multiples - 10 points, 2 points each
1. Write down the first five multiples of 12
2. What is the LCM of 12 and 8?
3. Write down all the factors of 50
4. Write down all the factors of 18
5. What is the HCF of 50 and 18
1. Write down the first five multiples of 12
2. What is the LCM of 12 and 8?
3. Write down all the factors of 50
4. Write down all the factors of 18
5. What is the HCF of 50 and 18
Squares and cubes - 5 points
Give me the answers to these:
1. 8 squared
2. 3 cubed
3. 12 squared
4. Square root of 81
5. Cubed root of 64
Give me the answers to these:
1. 8 squared
2. 3 cubed
3. 12 squared
4. Square root of 81
5. Cubed root of 64
Extra Credit
Short answer questions - 10 points, 2 points each
1. Explain what makes 2 a special prime number.
2. Why is 1 not a prime number?
3. In your opinion is zero odd, even or neither? Give a reason for your choice (you can't be wrong here!)
4. Which two shapes have number types named after them, as discussed in the lesson?
5. In your own words, what is the definition of a multiple?
1. Explain what makes 2 a special prime number.
2. Why is 1 not a prime number?
3. In your opinion is zero odd, even or neither? Give a reason for your choice (you can't be wrong here!)
4. Which two shapes have number types named after them, as discussed in the lesson?
5. In your own words, what is the definition of a multiple?
Problem solving - 20 points, 5 points each
The following wordy problems involve factors or multiples in some way. Solve them using whatever method you wish and send me your answers. You do not need to send me your working out but it may help me to identify any mistakes you may make.
1. In her band, Johanna has to play the drum on every sixth beat and the cymbal on every tenth beat. Which is the first beat that she plays both?
2. Adrian is planning a picnic. He wants to buy an equal number of hot dogs and hot dog buns. Hot dogs come in packages of 12. The buns come in packages of eight. What is the fewest number of hot dogs and buns he can buy?
3. Lorna, Mary, Nancy, Opal, and Penny all work together on the school safety patrol. Lorna works every day, Mary works every second day, Nancy works every third day, Opal works every fourth day, and Penny works every fifth day. Today (Day 0) they all worked together. How many days will it be until they all work together again?
4. A choir contains 48 female singers and 64 males. The choir master is trying to arrange them into rows for a concert but, since they are singing different harmonies, he wants single sex rows (no mixed rows of male and female will be allowed.) What is the greatest number of people that can be in each row to achieve this?
The following wordy problems involve factors or multiples in some way. Solve them using whatever method you wish and send me your answers. You do not need to send me your working out but it may help me to identify any mistakes you may make.
1. In her band, Johanna has to play the drum on every sixth beat and the cymbal on every tenth beat. Which is the first beat that she plays both?
2. Adrian is planning a picnic. He wants to buy an equal number of hot dogs and hot dog buns. Hot dogs come in packages of 12. The buns come in packages of eight. What is the fewest number of hot dogs and buns he can buy?
3. Lorna, Mary, Nancy, Opal, and Penny all work together on the school safety patrol. Lorna works every day, Mary works every second day, Nancy works every third day, Opal works every fourth day, and Penny works every fifth day. Today (Day 0) they all worked together. How many days will it be until they all work together again?
4. A choir contains 48 female singers and 64 males. The choir master is trying to arrange them into rows for a concert but, since they are singing different harmonies, he wants single sex rows (no mixed rows of male and female will be allowed.) What is the greatest number of people that can be in each row to achieve this?