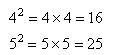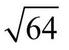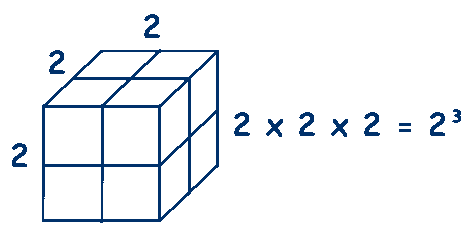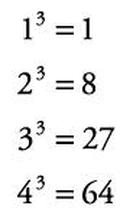Types of Number
This lesson is mostly definitions but there will be some stuff for you to do at the end so bear with me. All the types of numbers listed below are what I would consider essential knowledge for anyone wanting to improve their mathematical understanding.
Odd, Even and Zero
- Even Numbers are those in the two times table. They end in 2, 4, 6, 8, or 0 with the pattern repeating forever. Any even number can be divided by two with no remainder. If you add together two even numbers you get another even number.
- Odd numbers are the numbers which aren't in the two times table. They end in 1, 3, 5, 7 or 9 fitting nicely in the gaps left behind by the even numbers. If you divide an odd number by 2 you get a decimal answer.
- Zero has caused much debate amongst mathematicians as to whether it is odd or even. It is not in the two times table, which starts 1 x 2 = 2, but when you divide it by 2 you don't get a remainder (0 ÷ 2 = 0). I personally class it with the even numbers but really it is nothing so shouldn't be odd or even!
Prime Numbers
Prime numbers are especially important in mathematics due to their unique properties and large prime numbers are used to encrypt files and make internet transactions secure.
There are several definitions of prime numbers but the one I find most useful is that prime numbers have "exactly two factors... one and themself". I'm going to go into more detail on factors later in this lesson but basically this means that there are no other numbers which can be divided into a prime other than 1 and the prime itself. For example 7 is a prime number since it only appears in the 1 times table and the 7 times table.
The first ten prime numbers are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 ...
NOTE:
Prime numbers are especially important in mathematics due to their unique properties and large prime numbers are used to encrypt files and make internet transactions secure.
There are several definitions of prime numbers but the one I find most useful is that prime numbers have "exactly two factors... one and themself". I'm going to go into more detail on factors later in this lesson but basically this means that there are no other numbers which can be divided into a prime other than 1 and the prime itself. For example 7 is a prime number since it only appears in the 1 times table and the 7 times table.
The first ten prime numbers are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 ...
NOTE:
- Two is the only even prime number since all other even numbers have two as a factor and so are not prime!
- One is not a prime number since it only has one factor. This often causes confusion amongst non-mathematicians but trust me... one is not a prime number.
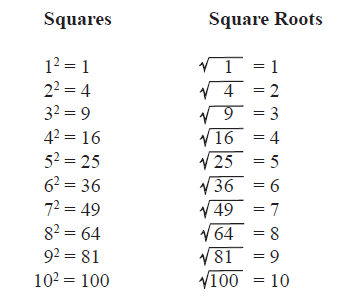
Square Numbers and Square Roots
If you completed the lesson on Multiplication you have already seen the square numbers although I didn't mention them at the time. A square number is the answer when a number is multiplied by itself, meaning it is the diagonal line down the middle of a multiplication grid. The mathematical symbol for a square number is a small 2 floating in the air just to the right of the number like this:
If you completed the lesson on Multiplication you have already seen the square numbers although I didn't mention them at the time. A square number is the answer when a number is multiplied by itself, meaning it is the diagonal line down the middle of a multiplication grid. The mathematical symbol for a square number is a small 2 floating in the air just to the right of the number like this:
The name "square number" comes from the fact that you can arrange each as a pattern of dots which forms a square:
It is worth learning the square numbers up to 12 squared (or 15 squared if you can) as it will help to speed up your multiplication.
A square root is the opposite of a square number. Basically you are undoing the sum and going back to the start. The symbol for a square root looks like a tick with a horizontal line which extends over a number like this:
If you know your square numbers then you can do square roots!
NOTE:
NOTE:
- You can find square roots of numbers which aren't square numbers using your calculator but you may need to round your answer
- If you try to square root a negative number on a calculator it will show up as an error. This is because square rooting negatives is a separate branch of mathematics called imaginary numbers. Don't worry about this, you won't need to know it unless you go onto do some more advanced Mathematics classes.
Cube Numbers
One step further than square numbers are cube (or cubed) numbers. They get their name from the fact that you can arrange them to make the 3D shape of a cube. To calculate a cube number you need to multiply something together three times. This is not the same as multiplying by 3, rather you multiply it by itself to get the square number, then by itself again to get the cube number
One step further than square numbers are cube (or cubed) numbers. They get their name from the fact that you can arrange them to make the 3D shape of a cube. To calculate a cube number you need to multiply something together three times. This is not the same as multiplying by 3, rather you multiply it by itself to get the square number, then by itself again to get the cube number
The opposite of a cube number is a cube (or cubed) root. Just like the square root this is about undoing the sum to get back to the start value. So, for example, the cubed root of 8 is 2.
Another two definitions that my students always get the wrong way around are factors and multiples. Maybe it's because they're always taught together... sorry I'm not going to break the habit of a lifetime!
Factors
I mentioned factors about when defining a prime number. In basic terms a factor is a number that goes into another number. People often talk of 'factor pairs' because the factors are the multiplications that make up the number. Factors are always smaller than the number you start with. Maybe this is best with an example:
The factors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24. This is because 1 x 24 = 2 x 12 = 3 x 8 = 4 x 6 = 24.
Usually I write factors in numerical order but this isn't really important other than helping me to keep organised and helping to ensure I don't miss any out. Writing factor pairs can be particularly useful as when I reach 4 x 6 and I know that 5 isn't a factor of 24 I know I can stop. I don't need to check the 6 times table as I've already got 6 and all the higher factors.
Square numbers are special in the fact that they have an odd number of factors (e.g. the factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18 and 36) since we don't list the square root twice in our factor list..
Prime numbers, as already mentioned, must have two factors.
I mentioned factors about when defining a prime number. In basic terms a factor is a number that goes into another number. People often talk of 'factor pairs' because the factors are the multiplications that make up the number. Factors are always smaller than the number you start with. Maybe this is best with an example:
The factors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24. This is because 1 x 24 = 2 x 12 = 3 x 8 = 4 x 6 = 24.
Usually I write factors in numerical order but this isn't really important other than helping me to keep organised and helping to ensure I don't miss any out. Writing factor pairs can be particularly useful as when I reach 4 x 6 and I know that 5 isn't a factor of 24 I know I can stop. I don't need to check the 6 times table as I've already got 6 and all the higher factors.
Square numbers are special in the fact that they have an odd number of factors (e.g. the factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18 and 36) since we don't list the square root twice in our factor list..
Prime numbers, as already mentioned, must have two factors.
Highest Common Factor
If you have a list of factors for two numbers, the highest common factor (often shortened to HCF) is the highest factor that is in both lists. For example:
The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18 and 36
The factors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24.
The HCF of 24 and 36 is 12 since it is the highest number in both factor lists.
NOTE:
If you have a list of factors for two numbers, the highest common factor (often shortened to HCF) is the highest factor that is in both lists. For example:
The factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18 and 36
The factors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24.
The HCF of 24 and 36 is 12 since it is the highest number in both factor lists.
NOTE:
- In the US this is often refered to as the greatest common factor (GCF) or greatest common divisor (GCD) instead of the UK version I teach (sorry, I'm from the UK, it's how I think!)
- Two numbers may have more than one factor in common but it is always the greatest/highest number mathematicians are interested in.
Multiples
To me, multiples reminds me of the word multiply and this is exactly what multiples are. When listing multiples you are listing the numbers in that times table (which is why tables are so important!) and so a multiple is always larger than the number you start with. For example:
The first five multiples of 7 are: 7, 14, 21, 28 and 35.
The first five multiples of 13 are: 13, 26, 39, 52, 65.
The list of multiples could go on forever so you will usually be asked only to write down the first few.
To me, multiples reminds me of the word multiply and this is exactly what multiples are. When listing multiples you are listing the numbers in that times table (which is why tables are so important!) and so a multiple is always larger than the number you start with. For example:
The first five multiples of 7 are: 7, 14, 21, 28 and 35.
The first five multiples of 13 are: 13, 26, 39, 52, 65.
The list of multiples could go on forever so you will usually be asked only to write down the first few.
Lowest/Least Common Multiple
If you have a list of muliples for two numbers, the lowest common multiple (LCM) is the lowest number in both the lists. It would not make sense to look for the highest number in this cases since your list of multiples can go on forever. For example
The LCM of 3 and 9 is 9 (3, 6, 9.... and 9...)
The LCM of 3 and 5 is 15 (3, 6, 9, 12, 15... and 5, 10, 15...)
The LCM can be useful in problem solving when you want to minimise something (see the extra credit section of your homework to see what I mean by this!).
If you have a list of muliples for two numbers, the lowest common multiple (LCM) is the lowest number in both the lists. It would not make sense to look for the highest number in this cases since your list of multiples can go on forever. For example
The LCM of 3 and 9 is 9 (3, 6, 9.... and 9...)
The LCM of 3 and 5 is 15 (3, 6, 9, 12, 15... and 5, 10, 15...)
The LCM can be useful in problem solving when you want to minimise something (see the extra credit section of your homework to see what I mean by this!).
I think that's enough for this lesson, sorry it was very heavy on definitions and contained lots of things for you to remember. Now... on to the homework...